Tutorial de Python Tight-Binding (ESP)
Python Tight-Binding es una librería que permite simular modelos tight-binding aprovechando la flexibilidad que ofrece Python. Si deseas familiarizarte en detalle con ella, puedes consultar la página de los autores: PythTB. Aquí encontrarás una descripción breve de cómo usarla a través de un ejemplo: grafeno. La descripción que haremos será básica por lo que enunciaré funcionalidades elementales para ganar confianza.
Este paquete es completamente funcional en las tres grandes plataformas (macOS, Windows, Linux). La guía de instalación la puedes encontrar aquí.
En este link está el script de Python que describe esta guía.
1. Pensando el sistema a realizar
Hay que tener en mente, de manera clara, cuál es el sistema que se quiere diseñar. Python Tight-Binding permite diseñar dos tipos de sistemas:
- Sistemas completamente finitos: Sistemas en donde se monta la red tight-binding con sus sitios y hoppings, obtiene una representación matricial finita en la base de orbitales dentro de una geometría definida.
- Sistemas con condiciones de borde periódicas: Sistemas en donde a partir de la definición de una celda unidad y mediante el teorema de Bloch, se entrega una representación matricial finita en el espacio de orbitales, pero que es translacionalmente invariante en una dada dirección. En estos sistemas podemos definir el espectro usando el cuasimomento adecuado en \(\mathbf{k}\) la dirección de periodicidad. En este tipo de sistemas podemos obtener las típicas estructuras de bandas \(E(\mathbf{k})\).
Para comenzar, importamos librerías útiles, entre ellas numpy, matplotlib y por supuesto pythtb:
import numpy as np
from matplotlib import pyplot as plt
from pythtb import *
2. Ejemplo: Grafeno con condiciones de borde abiertas (trozo de grafeno)
Estrictamente hablando, se entiende como grafeno a una lámina infinita de átomos de carbono dispuestos en un patrón hexagonal y de un átomo de espesor. Lo que vamos a hacer, inicialmente, es un trozo finito de grafeno en forma de rombo y veremos cómo obtener el espectro.
2.1. Definiendo la red
Tal como en un curso de física del sólido, una red cristalina se describe por un conjunto de vectores primitivos que definen la red de Bravais y una base. En Python Tight-Binding seguimos la misma lógica. Vamos a definir los vectores de red primitiva como
\[\begin{aligned} \mathbf{a}_1 &= \frac{1}{2}\hat{x} -\frac{\sqrt{3}}{2}\hat{y},\\ \mathbf{a}_2 &= \frac{1}{2}\hat{x} + \frac{\sqrt{3}}{2}\hat{y}. \end{aligned}\]Ahora tenemos que agregar la base para poder desarrollar la estructura hexagonal típica
\[\begin{aligned} \mathbf{v}_1 &= 0\hat{x} + \frac{1}{\sqrt{3}}\hat{y},\\ \mathbf{v}_2 &= 0\hat{x} + \frac{2}{\sqrt{3}}\hat{y}, \end{aligned}\]al orbital ubicado en \(\mathbf{v}_1\) le llamaremos \(A\) y al orbital ubicado en \(\mathbf{v}_2\) como \(B\). Representemos esto en un dibujo para tener una noción concreta de los vectores:
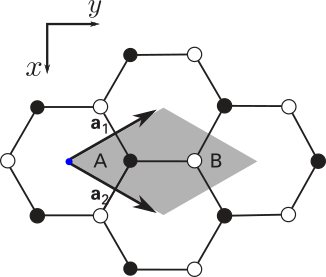
Nota: Dada esta definición, podemos notar que la constante de red está fijada por \(1/\sqrt{3}\approx 0.577\). La constante de red del grafeno en unidades físicas es \(a\approx 1.42\overset{\lower.5em\circ}{\mathrm{A}}\).
Recuerden: La elección de estos vectores y base no son únicas. Mientras mantengan la consistencia de la red (es decir, logren la forma hexagonal y la terminación adecuada) y tengan controlada la longitud característica entre carbonos, no hay problema.
Una vez definida la geometría de la red que deseamos construir (hasta ahora, en el papel), convierte recordar que en general, cualquier punto de red puede ser descrito como combinación lineal de los vectores de red
\[\mathbf{R} = n \mathbf{a}_1 +m \mathbf{a}_2,\]con \(m,n\) racionales. Esta es la forma de ubicar puntos en Python Tight-Binding. Ubicamos cualquier punto mediante coordenadas reducidas usando [n,m].
Para que PythTB pueda interpretar la red, declaramos los dos arreglos:
-
lat: arreglo que alberga el vector \(\mathbf{a}_1\) y \(\mathbf{a}_2\), es decir, los vectores de red en coordenadas cartesianas. -
orb: la ubicación de los orbitales que representan a \(\mathbf{v}_1\) y \(\mathbf{v}_2\) en coordenadas reducidas. Les dejo como ejercicio demostrar que
-
tb_model(dim_k, dim_r, lat, orb): declaramos la geometría de nuestro modelo usando el métodotb_modelque recibe la dimensión del espacio recíprocodim_k, del espacio realdim_ry los vectores de red y base.
¿Por qué necesitamos definir la dimensión del espacio recíproco si haremos un trozo finito? La lógica de PythTB es definir primero un sistema completamente infinito y posteriormente declararemos los cortes que definen la región que queremos estudiar.
Para terminar de montar la geometría de la red como hemos descrito, hacemos
lat = [[1/2, np.sqrt(3)/2], [-1/2, np.sqrt(3)/2]]
orb = [[1/3, 1/3], [2/3, 2/3]]
dim_k = 2
dim_r = 2
mi_grafeno = tb_model(dim_k, dim_r, lat, orb)
Una vez que los atributos geométricos están declarados, debemos poner los elementos físicos en la grilla.
2.2. Definiendo los parámetros físicos
Para que esto tenga sentido físico alguno, hemos de incorporar las energías de sitio y los hoppings entre ellos, que son los bloques que construyen cualquier red tight-binding. Con esta prescripción PythTB desarrollará la presentación matricial por nosotros.
2.2.1 Energía de sitio
En principio, en el grafeno no tenemos la necesidad de poner energía de sitio, es decir podemos hacer
# Parametros de energia de sitio
delta = 0
mi_grafeno.set_onsite([-delta, delta])
El método set_onsite lo que hace es colocar una energía de sitio al orbital de tipo \(A\) con -delta y al orbital de tipo \(B\) delta. Si declaramos un delta no nulo, se induciría sobre nuestro grafeno un término de masa tipo Semenoff (o también conocido como potencial de staggering).
2.2.2 Hoppings
Esto corresponde a la integral de intercambio entre orbitales vecinos (en este caso los orbitales que contribuyen a las propiedades electrónicas). En el grafeno esto lo representamos como un término que conecta primeros vecinos. Fijaremos esta energía en t=-1. El código que hace esto es:
# Parametros de hoppings
t = -1
mi_grafeno.set_hop(t, 0, 1, [ 0, 0])
mi_grafeno.set_hop(t, 1, 0, [ 1, 0])
mi_grafeno.set_hop(t, 1, 0, [ 0, 1])
¿Cómo funciona esto? La sintaxis es:
(amplitud, sitio_tipo_i, sitio_tipo_j, [vector_desde_sitio_tipo_j_en_reducidas])
En el primer hopping declarado, le hemos dicho a PythTB que dibuje un hopping desde el sitio cero (tipo \(A\)) al sitio uno (tipo \(B\)) dentro de la celda unidad [0, 0] con amplitud \(t=-1\). La misma lógica se sigue para los otros hoppings. Mediante el método set_hop se repite la construcción de todos los hoppings equivalentes en la red.
mi_grafeno.display()
Lo que en nuestro caso entregará en la terminal un resumen del sistema recién armado:
# En la terminal saldra esto
---------------------------------------
report of tight-binding model
---------------------------------------
k-space dimension = 2
r-space dimension = 2
number of spin components = 1
periodic directions = [0, 1]
number of orbitals = 2
number of electronic states = 2
lattice vectors:
# 0 ===> [ 0.5 , 0.866 ]
# 1 ===> [ -0.5 , 0.866 ]
positions of orbitals:
# 0 ===> [ 0.3333 , 0.3333 ]
# 1 ===> [ 0.6667 , 0.6667 ]
site energies:
# 0 ===> 0.0
# 1 ===> 0.0
hoppings:
< 0 | H | 1 + [ 0 , 0 ] > ===> -1.0 + 0.0 i
< 1 | H | 0 + [ 1 , 0 ] > ===> -1.0 + 0.0 i
< 1 | H | 0 + [ 0 , 1 ] > ===> -1.0 + 0.0 i
hopping distances:
| pos( 0 ) - pos( 1 + [ 0 , 0 ] ) | = 0.5774
| pos( 1 ) - pos( 0 + [ 1 , 0 ] ) | = 0.5774
| pos( 1 ) - pos( 0 + [ 0 , 1 ] ) | = 0.5774
2.3 Condiciones de borde
Ahora debemos especificar si queremos un sistema finito, o infinito o finito solo en una dirección, etc. Como es de nuestro interés solamente hacerlo finito, vamos a cortar en las dos direcciones y no pegar los bordes:
mi_grafeno_int = mi_grafeno.cut_piece(10, 0, glue_edgs = False)
mi_grafeno_fin = mi_grafeno_int.cut_piece(10, 1, glue_edgs = False)
La descripción de esto es:
(numero_de_celdas_de_ancho, direccion_no_periodica, pegar_bordes)
- En nuestro caso, hemos acordado que vamos a cortar nuestro grafeno (infinito hasta ahora) y haremos que la dirección cero, dada por \(\mathbf{a}_1\), no periódica. Esto definiría una cinta (un ribbon) en el caso de que preservemos la otra dirección como periódica. El ancho de la cinta es hasta ahora ahora de ancho 10 celdas unidad y periódico en \(\mathbf{a}_2\). A este sistema le hemos llamado
mi_grafeno_int. Notar que no hemos pegado los bordes. Si lo hiciéramos estaríamos imponiendo periodicidad en esa dirección. - Luego hacemos lo mismo para la dirección \(\mathbf{a}_2\), resultado en un rombo de grafeno, finito. A este sistema le hemos llamado
mi_grafeno_fin.
3. Extraer información física
El sistema ya está montado y PythTB ya hizo su trabajo. En adelante, queda determinar ya sea la energía o los estados (y manipular la información obtenida de la manera que gusten!). Por ejemplo, obtengamos los autovalores y autoestados y grafiquemos para el autoestado ed = 5 (por decir algo, ustedes pueden elaborar sus rutinas para buscar lo que deseen) y ploteamos la amplitud de probabilidad en el sistema que elaboramos:
# Encontrar el espectro del Hamiltoniano
(evals, evecs) = mi_grafeno_fin.solve_all(eig_vectors = True)
# Buscamos algun autovalor y su respectivo autoestado
ed = 5
energia = evals[5]
ev = evecs[ed, :]
(fig, ax) = mi_grafeno_fin.visualize(0, 1, eig_dr = ev, draw_hoppings = True)
ax.set_title(r"Estado para $E \approx$"+ str(round(energia, 2))+ " en un rombo de grafeno")
ax.set_xlabel("Coordenada, $x$")
ax.set_ylabel("Coordenada, $y$")
ax.set_ylim([-0.5, 17])
ax.set_xlim([-5, 5])
fig.tight_layout()
fig.savefig("edge_state.pdf")
El método visualize entrega una forma de ver el sistema que construyeron junto con la densidad de probabilidad de un determinado estado (color negro). El punto azul solo denota el origen y no tiene otro significado físico. Si desean graficar la información por sus propios medios, solo deben operar con los vectores entregados en evecs y con los autovalores en evals. Esto es solo una demostración elemental. A continuación el gráfico entregado por el bloque anterior de código
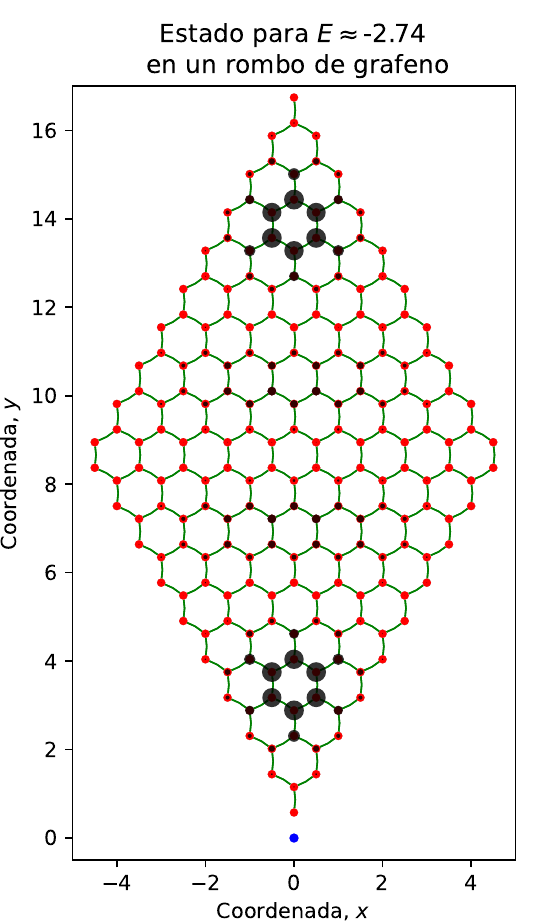
Para embellecer estos gráficos de manera sustancial, escribiré un post en el futuro.
4. Observaciones finales
- En esta ocasión hemos visto como calcular propiedades con respecto a sistemas finitos. Para calcular la estructura de bandas de sistemas infinitos hay que pegar los bordes necesarios.
- Periodicidad en una sola dirección es sencillo pues hay solo un índice \(k\) entonces podemos graficar \(E(k)\) al extraer el espectro adecuadamente.
- Periodicidad en dos direcciones es complicado, pues ahora tenemos \(k_x\) y \(k_y\), por lo que tenemos una estructura tipo \(E(k_x,k_y)\). La prácticas usuales para estos casos son hacer la estructura de bandas en paths conectando mediante alguna serie de caminos puntos importantes del espacio recíproco, o derechamente hacer alguna representación en 3D de la función (curvas de nivel, superficies, etc). Vean los ejemplos aquí en donde aparece el enfoque de los paths conectando puntos \(\Gamma,M, K'\) etc.
4.1 Estructuras de bandas, una dirección de periodicidad
Con los elementos que hemos visto aquí el tutorial está finalizado. Como recomendación para orientar un cálculo de estructuras de bandas, recomiendo ver el primer ejemplo en la librería de ejemplos: Simple example el que pueden encontrar aquí.
4.2 Métodos útiles
PythTB ofrece una serie de métodos útiles, aquí escribo una breve reseña de dos que me parecen particularmente útiles:
4.2.1 model.get_orb()
Esto entrega un objeto iterable por todos los sitios del modelo model. Cada elemento de este iterable almacena las coordenadas cartesianas de los sitios. Por ejemplo, para imprimir cada una de ellas:
for site in modelo.get_orb():
pos_x = site[0]
pos_y = site[1]
print (pos_x, pos_y)
4.2.2 modelo_nuevo = modelo.remove_orb(orbitals)
Este método lo que hace es borrar el orbital del modelo modelo y el nuevo sistema sin ese orbital es modelo_nuevo. La variable orbitals debe ser un arreglo (puede tener uno o varios orbitales).
Cuidado: Al remover sitios están redefiniendo el sistema. Por lo que los índices de todos los sitios cambian!